Visualization of bird sound files on amplitudes¶
In [1]:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import os
from pydub import AudioSegment
from scipy import signal
from scipy.io import wavfile
In [2]:
# custom matplotlib style
usetex = True
fontsize = 14
params = {'axes.labelsize': fontsize + 2,
'font.size': fontsize + 2,
'legend.fontsize': fontsize + 2,
'xtick.labelsize': fontsize,
'ytick.labelsize': fontsize}
#'text.usetex': usetex} # Requires latex on the computer
plt.style.use('ggplot')
plt.rcParams.update(params)
Pre-processing¶
Conversion: MP3 to WAV¶
Here, we take all the MP3 bird sounds inside the "ALL BIRDS" and "Test Birds from Kasios" folders, and convert them into WAV files.
We have to do this because WAV is the most supported format to do sound processing.
Please put the folders "ALL BIRDS" and "Test Birds from Kasios" of the VAST challenge in the folder "data".
This step will take some minutes.
In [3]:
from data.loader import get_kasios_obs, get_obs, map_path
df = get_obs(songs = True)
df_kasios = get_kasios_obs(songs = True)
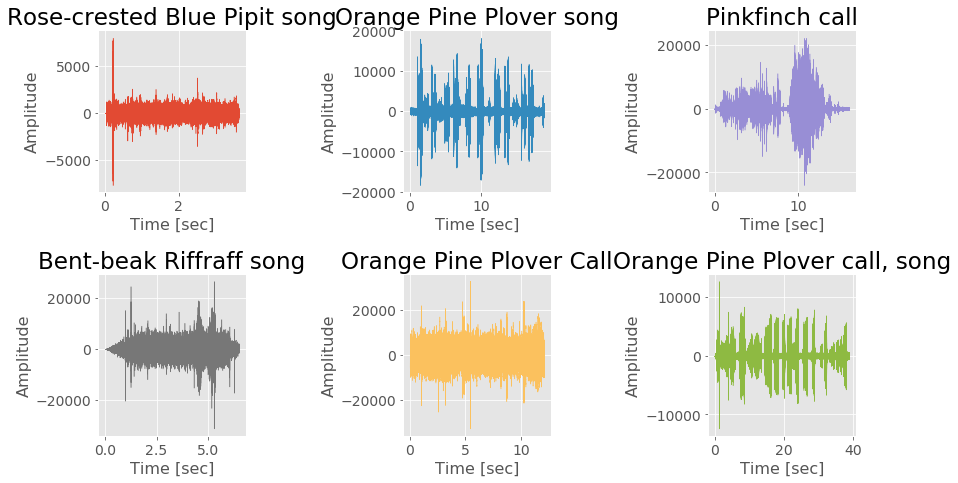
Visualization¶
Temporal representation¶
In [4]:
# take random samples
samples = df.sample(6)
fig = plt.figure(figsize=(13,7))
for i, (index, obs) in enumerate(samples.iterrows()):
# read wav file
rate, data = wavfile.read(obs["song"])
times = np.arange(len(data))/float(rate)
title = '{} {}'.format(obs["English_name"], obs["Vocalization_type"])
ax = fig.add_subplot(2, 3, i+1)
ax.fill_between(times, data, color="C{}".format(i)) # plot the signal
ax.set_title(title)
ax.set_xlabel('Time [sec]')
ax.set_ylabel('Amplitude')
plt.tight_layout()
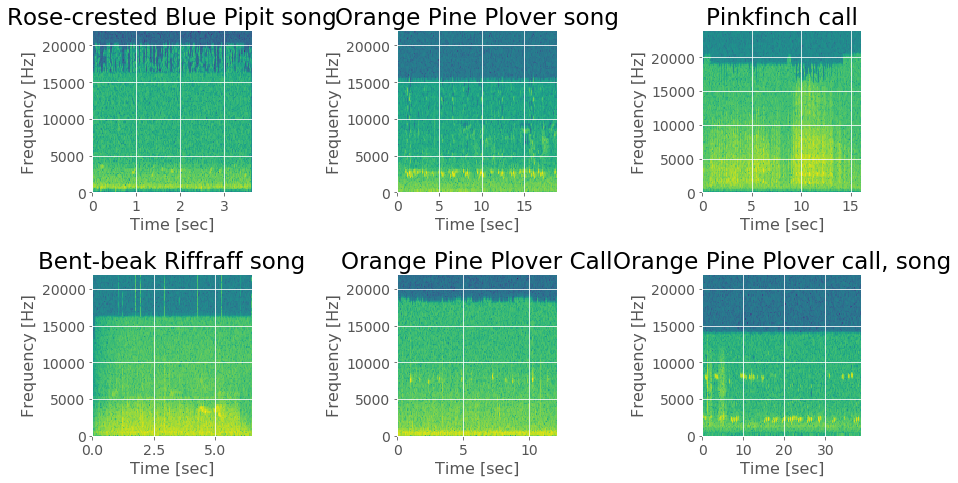
Frequency representation (2D spectrogram)¶
In [5]:
fig = plt.figure(figsize=(13,7))
for i, (index, obs) in enumerate(samples.iterrows()):
# read wav file
rate, data = wavfile.read(obs["song"])
times = np.arange(len(data))/float(rate)
title = '{} {}'.format(obs["English_name"], obs["Vocalization_type"])
ax = fig.add_subplot(2, 3, i+1)
ax.specgram(data, Fs=rate)
ax.set_title(title)
ax.set_xlabel('Time [sec]')
ax.set_ylabel('Frequency [Hz]')
plt.tight_layout()
Please check the notebook "4_spectral_analysis.ipynb"
Analyze Kasios test birds with visualizations¶
Kasios provided 15 birds sounds. According to them, they are songs and calls from the Rose-crested Blue Pipit species.
Aim: Analyse the Kasios birds tests records and verify from which species each record belongs.
The dataset we have been provided contains 186 samples of Rose-crested Blue Pipits sounds. They are "songs" and "calls", with different qualities, graded from A to E. Most of them are in good quality. In fact, quality A and B represent 148 records.
We will first visualize some of the Blue Pipits records to identify some characteristics, and then we will compare what we obtained with the Kasios records.
To do the comparison, we will plot all the records with the same scales. The time (x-axis) will go from 0 to 20 seconds, and the amplitude (y-axis) from -10000 to 10000.
In [6]:
def plot_signal_temp(df, title):
fig = plt.figure(figsize=(13,9))
fig.suptitle(title)
for i, (index, obs) in enumerate(df.iterrows()):
# read wav file
rate, data = wavfile.read(obs["song"])
times = np.arange(len(data))/float(rate)
title = '{} {}'.format(obs["English_name"], obs["Vocalization_type"])
# plot the signal
ax = fig.add_subplot(3, 3, i+1)
times = np.arange(len(data))/float(rate)
ax.fill_between(times, data, color="C{}".format(i))
ax.set_xlabel('Time [sec]')
ax.set_ylabel('Amplitude')
ax.set_xlim(0, 20)
ax.set_ylim(-10000, 10000)
fig.tight_layout(rect=[0, 0.03, 1, 0.95])
def plot_spectrogram(df, title):
fig = plt.figure(figsize=(13,9))
fig.suptitle(title)
for i, (index, obs) in enumerate(df.iterrows()):
# read wav file
rate, data = wavfile.read(obs["song"])
times = np.arange(len(data))/float(rate)
title = '{} {}'.format(obs["English_name"], obs["Vocalization_type"])
# plot the spectrogram
ax = fig.add_subplot(3, 3, i+1)
ax.specgram(data, Fs=rate)
ax.set_xlabel('Time [sec]')
ax.set_ylabel('Frequency [Hz]')
ax.set_xlim(0, 20)
fig.tight_layout(rect=[0, 0.03, 1, 0.95])
Blue Pipit songs¶
In [7]:
df_bp_songs = df.loc[(df['English_name'] == 'Rose-crested Blue Pipit')
& (df['Vocalization_type'] == 'song')
& (df['Quality'] == 'A')]
df_bp_songs = df_bp_songs[:9]
display(df_bp_songs)
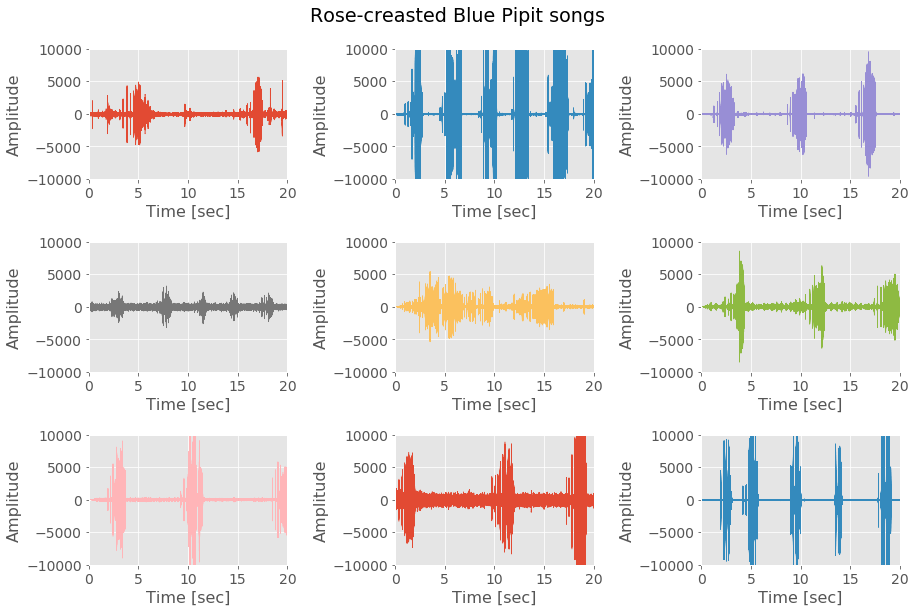
plot_signal_temp(df_bp_songs,
title='Rose-creasted Blue Pipit songs')
We notice that the songs of the Blue Pipit consist in sequences of "song - silence" repetitions, that occur at intervals of equal length.
In the different records, the time of silence varies, but the time of the songs is approximately the same (2 seconds).
The amplitude of the song periods is going crescendo.
In the different records, the time of silence varies, but the time of the songs is approximately the same (2 seconds).
The amplitude of the song periods is going crescendo.
Blue Pipit calls¶
In [8]:
df_bp_calls = df.loc[(df['English_name'] == 'Rose-crested Blue Pipit')
& (df['Vocalization_type'] == 'call')
& (df['Quality'] == 'A')]
df_bp_calls = df_bp_calls[:9]
display(df_bp_calls)
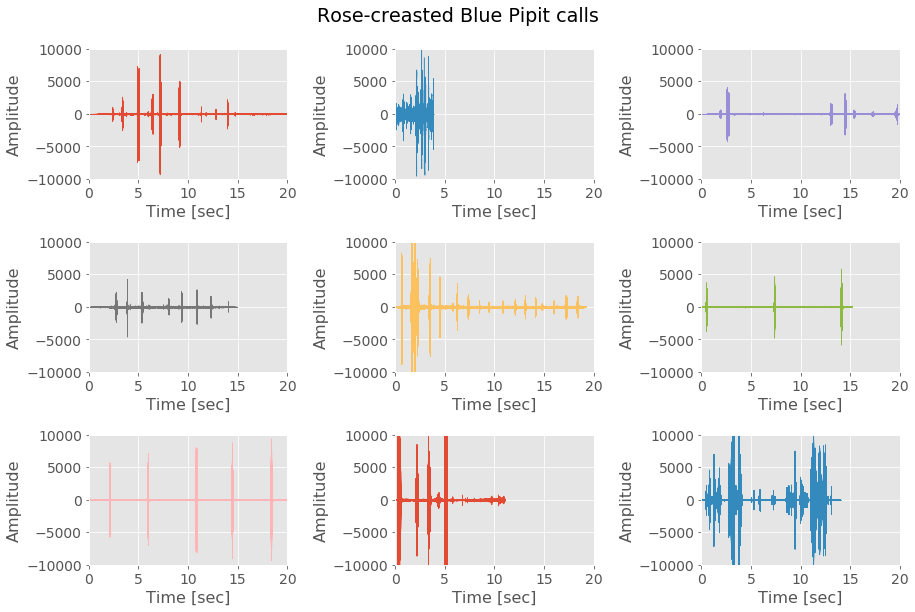
plot_signal_temp(df_bp_calls,
title='Rose-creasted Blue Pipit calls')
From this plot, we can guess the shape of the Blue Pipits calls.
We can distinguish the repetition of high amplitude picks followed by silences.
These picks events are the calls. They happen at regular intervals.
We can distinguish the repetition of high amplitude picks followed by silences.
These picks events are the calls. They happen at regular intervals.
To conclude, the difference between songs and calls of the Blue Pipit is the fact that
the songs are longer vocalizations which usually include a variety of notes in a sequence, while bird calls are short communications which are often single notes.
Kasios files¶
In [9]:
# Get all tests sounds of Kasios
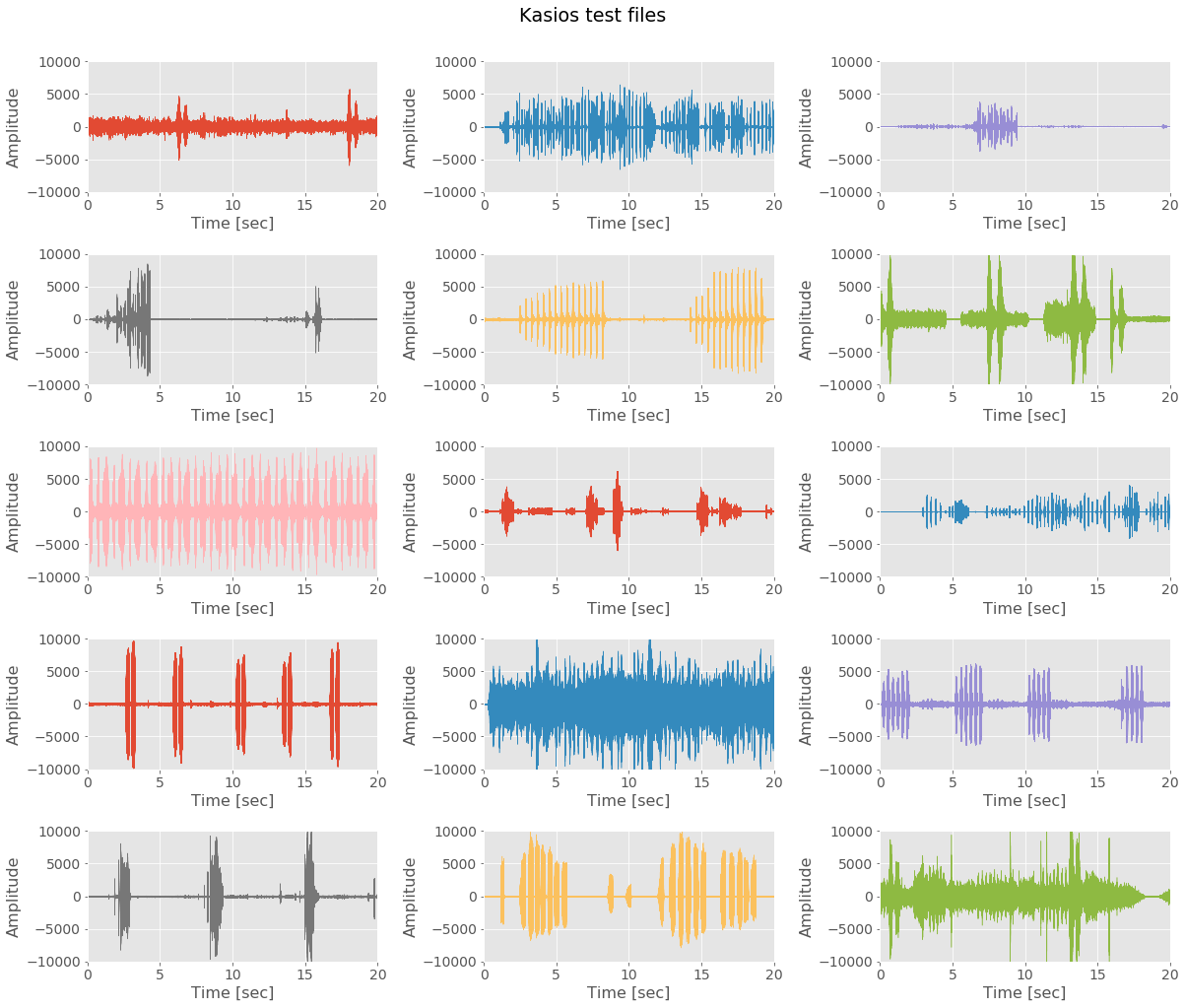
fig = plt.figure(figsize=(17,15))
fig.suptitle('Kasios test files')
for i, (index, obs) in enumerate(df_kasios.iterrows()):
# read wav file
rate, data = wavfile.read(obs["song"])
# plot the signal
ax = fig.add_subplot(5, 3, i+1)
times = np.arange(len(data))/float(rate)
ax.fill_between(times, data, color="C{}".format(i%9))
ax.set_xlabel('Time [sec]')
ax.set_ylabel('Amplitude')
ax.set_xlim(0, 20)
ax.set_ylim(-10000, 10000)
fig.tight_layout(rect=[0, 0.03, 1, 0.95])
Here, we have plotted the 15 test sound of Kasios. They claim that these records are Blue Pipits records.
From the shapes of Blue Pipit songs and calls we have just described, we can say that most of the test files do not look like Blue Pipit records.
From the shapes of Blue Pipit songs and calls we have just described, we can say that most of the test files do not look like Blue Pipit records.
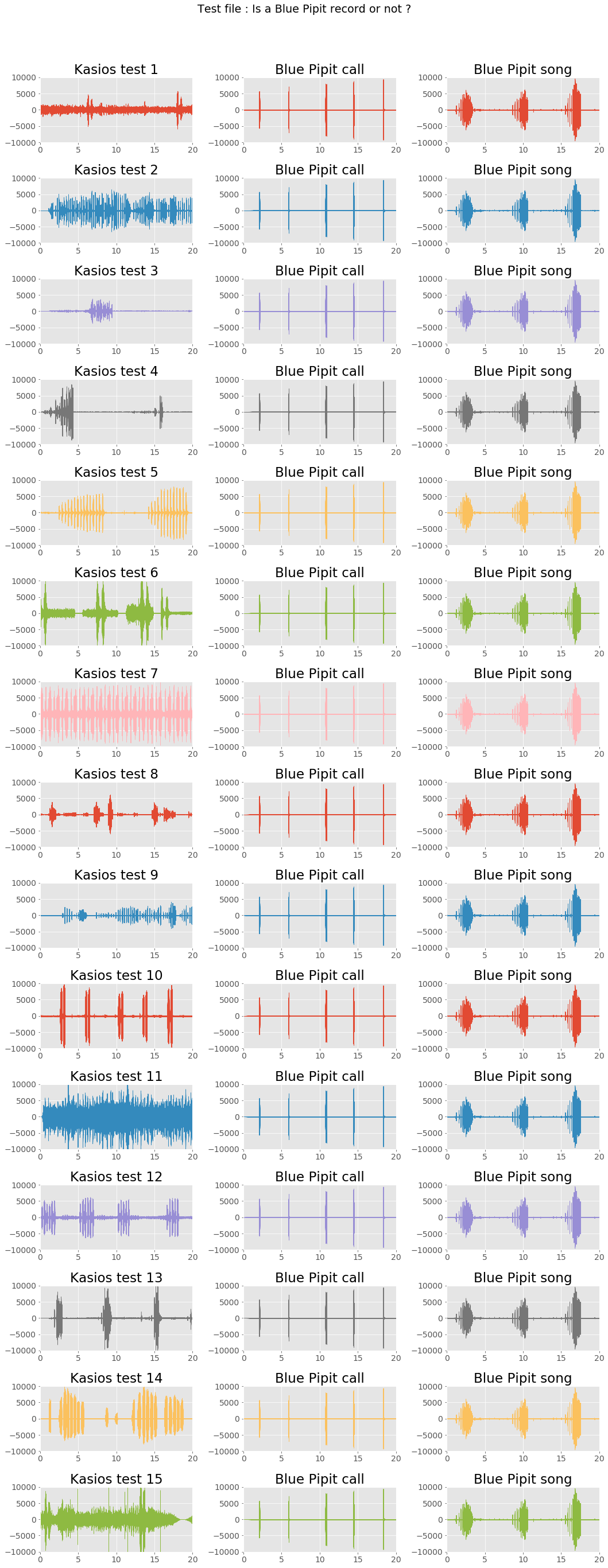
On the next plot, we emphasize this in focusing on each test sound one by one. We will try to say if it looks similar to a Blue Pipit call or song.
In [10]:
fig = plt.figure(figsize=(15,40))
fig.suptitle('Test file : Is a Blue Pipit record or not ?')
f = df.loc[368492].song
rate_calls, data_calls = wavfile.read(f)
f = df.loc[377874].song
rate_songs, data_songs = wavfile.read(f)
for i, (index, obs) in enumerate(df_kasios.iterrows()):
# read wav file
rate, data = wavfile.read(obs["song"])
# visualize the signals
ax = fig.add_subplot(15, 3, 3*i+1)
times = np.arange(len(data))/float(rate)
title = 'Kasios test {}'.format(i+1)
ax.fill_between(times, data, color="C{}".format(i%9))
ax.set_title(title)
ax.set_xlim(0, 20)
ax.set_ylim(-10000, 10000)
bx = fig.add_subplot(15, 3, 3*i+2)
times = np.arange(len(data_calls))/float(rate_calls)
bx.fill_between(times, data_calls, color="C{}".format(i%9))
bx.set_title('Blue Pipit call')
bx.set_xlim(0, 20)
bx.set_ylim(-10000, 10000)
cx = fig.add_subplot(15, 3, 3*i+3)
times = np.arange(len(data_songs))/float(rate_songs)
cx.fill_between(times, data_songs, color="C{}".format(i%9))
cx.set_title('Blue Pipit song')
cx.set_xlim(0, 20)
cx.set_ylim(-10000, 10000)
fig.tight_layout(rect=[0, 0.03, 1, 0.95])
| Test file | Looks similar to Blue Pipit |
|---|---|
| 1 | Yes |
| 2 | No |
| 3 | No |
| 4 | Maybe |
| 5 | No |
| 6 | No |
| 7 | No |
| 8 | No |
| 9 | No |
| 10 | No |
| 11 | Maybe |
| 12 | No |
| 13 | Yes |
| 14 | No |
| 15 | Yes |
Like we previously said, most of the test records from Kasios does not seem to be from the Rose-Crested-Blue-Pipit species. But we cannot be sure of the comparison as it is only made by visual interpretation. To be more accurate, we could do feature extraction on the spectral representation.
Check the notebook 4_spectral_analysis.ipynb.